
콘텐츠
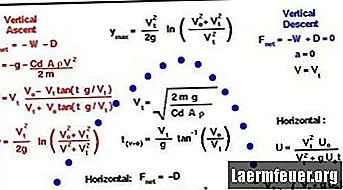
다음은 총알의 궤적, 특히 공중에서의 시간, 궤적의 범위 및 가장 높은 지점을 계산하는 방법입니다. 이 예에서는 계산을 단순화하기 위해 몇 가지 가정을했습니다. 무시할 수있는 공기 저항, 바람이없고 지구 자전이 적용되기에 불충분 한 발사 거리가 있습니다.
공중에서 시간을 결정하십시오.
1 단계
먼저 활의 모양을 결정해야합니다. 각도가 처음에 아래쪽이면 가장 높은 지점이 이미 발사 위치로 알려져 있습니다. 이 각도가 얕거나 충분한 높이 (h)인지 여부에 관계없이 위쪽 각도에서도 대상을 가장 높은 지점으로 지정할 수 있습니다. 이것은 방송 시간이 결정되는 4 단계에서 결정할 수 있습니다.
2 단계
각도 "?" 발사 속도는 발사체의 초기 궤적과 수평 사이의 속도이므로 초기 수직 속도는 V (i) = V.sen?입니다.
3 단계
공기 시간은 위치 방정식 h = V.sen? .T-(0.5) g.t ^ 2, 여기서 g = 9.8 미터 / 초 ^ 2. 공기 중의 시간 t를 제외한 모든 변수가 알려져 있으므로 2 차 함수를 사용하여 해결할 수 있습니다. ax ^ 2 + bx + c = 0, 따라서 x = [-b ± √ (b ^ 2-4ac )] / 2a
4 단계
t에 대해 둘 이상의 해가 허용되는 경우 h> 0이므로 첫 번째 결과는 상승 경로에서 높이 = h 일 때에 해당하고 두 번째 결과는 하강 경로에서 높이 = h 일 때에 해당합니다. h <0이면 t에 대한 유일한 실제 솔루션이 허용되고 다른 하나는 음수입니다.
최대 높이 결정
1 단계
<0이면 최대 높이가 초기 높이 인 h = 0임을 이미 알고 있습니다.
2 단계
총알이 h로 확장되는 시간 t가 두 번 이상있는 경우 가장 작은 t는 h가 가장 높은 지점 인 비행 경로에 해당합니다. 가장 높은 t는 h로 돌아 가기 전에 더 높은 높이에 도달 한 총알에 해당합니다.이 높이를 해결하려면 공식 V (t) = V (0)-9.8t를 사용하여 수직 속도가 다음과 같을 때 t의 값을 찾습니다. 제로. 즉, 몇시에 t, V.sen? = 9.8t.?
3 단계
t를 풀고 높이 공식을 연결하면 최대 높이가됩니다. hm = V.sen? -4.9t ^ 2. t에 대해 하나의 솔루션 만 허용되는 경우 동일한 접근 방식이 최대 높이 솔루션에 사용됩니다.
이동 한 수평 거리를 결정하십시오.
1 단계
총알이 높이 h에 도달 할 때까지 이동 한 수평 거리를 확인하려면 먼저 총알의 초기 수평 속도를 계산합니다. v (i) = V.cos (?).
2 단계
수평 속도를 사용하여 공식 위치에서 총알이 최종 높이 A에 도달 할 때 시간 t를 대입합니다. A = V.cosΘ.t. 오른쪽에 공기 저항과 가속 항이 없다고 가정합니다.
3 단계
높이가 h에있을 때 t가 한 번 이상 있으면 "A"의 두 위치가 유효하며 가장 높은 지점은 두 "A"중 작은 경우 hm입니다. 수평 및 수직 끝 위치와 도달 한 가장 높은 지점이 이제 알려져 총알의 궤적을 결정합니다.