변수를 사용하여 분수를 단순화하는 방법

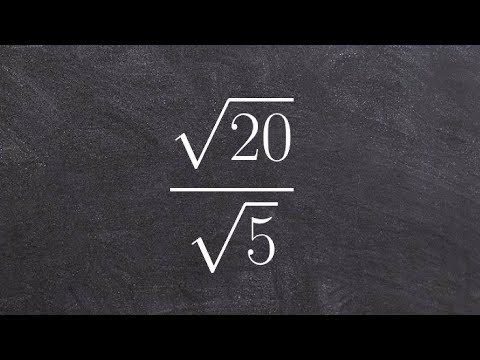
콘텐츠

지침
어떻게

학생들은 전형적으로 학교의 8 학년 또는 9 학년에서 대수 1 학년 중 변수를 사용하여 분수를 단순화하는 방법을 학습합니다. 분수를 성공적으로 단순화하기 위해서는 사전 지식이 필요합니다. 예를 들어 변수를 사용하지 않고 단순화 할 수 있어야하며 가장 큰 공통 요소 또는 MFC를 결정하는 것과 같은 기술을 포함하는 절차가 있어야합니다. 변수의 오른쪽 위의 색인에 쓰여있는 숫자 인 지수의 용어와 같은 용어도 알고 있어야합니다.

지침

변수로 분수를 단순화하는 것은 대수학의 초기 주제입니다. (Comstock 이미지 / Comstock / 게티 이미지)

분수 계수를 가장 낮은 항으로 줄입니다. 계수는 변수의 왼쪽에 나타나는 숫자입니다. 가장 작은 정도까지 줄이려면 두 값을 곱하는 가장 큰 숫자 인 MFC를 결정한 다음 분자와 분모를 그 수로 나누십시오. 예를 들어 문제 [6 (a ^ 4) (b ^ 2) c] / [9 (a ^ 4) (b ^ 5)]를 생각해보십시오. 계수는 6과 9이고 MFC는 3입니다. 분자를 3으로 나눈 값을 2로하고 분모를 3으로 나누면 3이되어 [2 (a ^ 4) (b ^ 2) c] / [ 3 (a ^ 4) (b ^ 5)].
동등한 지수를 갖는 변수를 취소하십시오. [a (4) (b ^ 2) c] / [3 (a ^ 4) (b ^ 5)]에서 변수 "a"는 지수 4를가집니다. 따라서 분자의 "a ^ 4" 분모에서 반복되는 "A ^ 4"표현식에서 변수 "a"를 제거하면 [2 (b ^ 2) c] / [3 (b ^ 5)]가됩니다.
분자의 변수의 분모에있는 변수의 지수를 뺍니다. 이 뺄셈을 한 후에 분자에 양의 지수를 가진 변수를 넣되 음의 지수를 가진 변수를 분모에 넣고 음의 지수를 양수로 변경합니다. [2 (b ^ 2) c] / [3 (b ^ 5)]에서 변수 b는 둘 다에 나타납니다. 지수 2 - 5 = 3을 뺍니다. 그래서 당신은 b ^ -3을가집니다. 이 지수가 음수이므로 분모에 넣으면 양수가됩니다. 이런 식으로 예제는 (2c) / (3b ^ 3)에 대해 단순화됩니다. 분자와 분모 모두에서 공통적 인 모든 변수에 대해이 과정을 반복합니다. 이 예제에서는 두 변수 사이에 반복 변수가 없기 때문에 (2c) / (3b ^ 3)이 최종 답입니다.