콘텐츠

정사각형을 만들고 두 개의 대각선을 그려야한다면, 그것들은 그 중심에서 교차하여 네 개의 직각 삼각형을 형성합니다. 두 선은 90도 각도로 교차합니다. 큐브의이 두 대각선이 각각 한 모서리에서 다른 모서리로 이어지고 중앙에서 교차 할 수 있다는 것을 직관적으로 발견 할 수 있습니다. 또한 직각으로 교차 할 수 있습니다. 하지만 그건 실수입니다. 두 대각선이 교차하는 각도를 결정하는 것은 처음 보는 것보다 약간 더 복잡하지만 기하학과 삼각법의 원리를 이해하는 것이 좋습니다.
1 단계
모서리 길이를 단위로 정의합니다. 정의에 따라 큐브의 각 가장자리는 수분과 같은 길이를 갖습니다.
2 단계
명료 함을 위해 피타고라스 정리를 사용하여 같은면의 한 모서리에서 다른 모서리로 이어지는 대각선의 길이를 결정합니다.이를 "부 대각선"이라고 부를 수 있습니다. 형성된 직각 삼각형의 각 변은 단위이므로 대각선은 √2와 같아야합니다.
3 단계
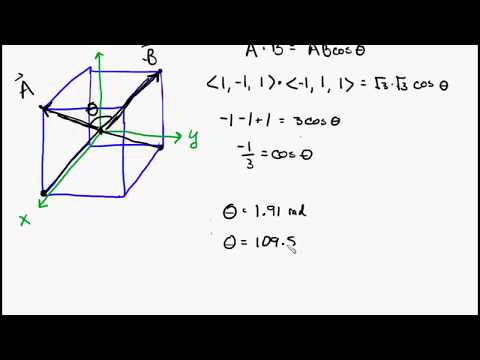
피타고라스 정리를 사용하여 큐브의 다른면에서 한 모서리에서 다른 모서리로 이어지는 대각선의 길이를 결정합니다.이를 "주 대각선"이라고 할 수 있습니다. 한면에 1 단위에 해당하는 직각 삼각형과 "작은 대각선"에 해당하는면이 있는데, 이는 두 단위의 제곱근에 해당합니다. 빗변의 제곱은 변의 제곱의 합과 같으므로 빗변은 √3이어야합니다. 큐브의 한쪽 모서리에서 다른 쪽 모서리로 이어지는 각 대각선은 √3 단위와 같습니다.
4 단계
정육면체의 중심을 가로 지르는 두 개의 큰 대각선을 나타내는 직사각형을 그리고 교차 각도를 찾아야한다고 생각합니다. 이 직사각형은 높이가 1 단위, 너비가 √2 단위 여야합니다. 더 큰 대각선은이 직사각형의 중심에서 교차하여 두 가지 유형의 삼각형을 형성합니다. 그들 중 하나는 1 단위와 같은 측면을 가지며 다른 두 개는 √3 / 2 (더 큰 대각선 길이의 절반)와 같습니다. 다른 하나는 √3 / 2와 같은 두 변을 가지지 만 첫 번째는 √2입니다. 삼각형 중 하나만 분석하고 첫 번째 삼각형을 선택하고 알려지지 않은 각도를 발견하면됩니다.
5 단계
이 삼각형의 알 수없는 각도를 구하려면 삼각 공식 "c² = a² + b²-2ab x cos C"를 사용하십시오. "C = 1", "b"및 "a"는 √3 / 2와 같습니다. 이 값을 방정식에 넣으면 각도의 코사인이 1/3이라는 것을 알 수 있습니다. 코사인 1/3의 역은 70.5도 각도에 해당합니다.