그래프에서 이차 부등식을 풀고 표현하는 법

콘텐츠

지침
어떻게
공지 사항
필요한 것

수학에서 불평등은 평등과 다르다. 불평등은 그것이 사실로 드러나는 특정한 숫자가 아닌 불평등을 만족시키는 일련의 반응을 묘사한다. 이차 방정식 (2 차 변수를 사용하는 방정식)이 선형 방정식 (직선에있는 방정식)보다 복잡하고 그래프의 불평등을 나타내는 것은 등가성에 대해 동일한 것을 수행하는 것보다 약간 복잡하므로 많은 학생들이 어려움을 겪습니다 그들은 두 개념을 결합해야한다는 것을 알게됩니다. 그러나 2 차 불평등을 차트로 작성하고 해결하는 데는 새로운 지식이 거의 필요하지 않으며 실습을 통해 쉽게 이해할 수 있습니다.

지침

2 차 부등식의 그래프를 만들 때 연필을 사용하여 오류를 지울 수 있습니다. (Fotolia.com에서 AGphotographer로 연필 이미지)

그래프 용지에 표준 직교 좌표계를 그리고 x (수평) 축과 y (수직) 축에 표시를 추가합니다.
표준 형식 (및 ax ^ 2 + bx + c)에서 2 차 부등식을 다시 작성하십시오. 예를 들어, y <5x - 3x ^ 2 + 8은 y <-3x ^ 2 + 5x + 8로 작성됩니다.
-b / 2a 공식을 사용하여 2 차항 불균형 그래프 (포물선이라고 함)의 정점 (높거나 낮은 점)의 x 값을 찾습니다. 예를 들어, y <-3x ^ 2 + 5x + 8 인 경우 5/6을 얻기 위해 -5/2 (-3)을 작성합니다.
방정식에서 정점의 x 값을 대체하여 정점의 y 값을 얻습니다. 이 경우 x 값으로 5/6이 y 값으로 145/12가됩니다. 그런 다음 정점을 (5/6, 145/12)로 작성하고 그 점을 그래프에 표시하십시오.
2 차 부등식을 같음으로 변경하고 0으로 동일하게 만듭니다. 방정식 y <5x - 3x ^ 2 + 8은 0 = - 3x ^ 2 + 5x + 8이됩니다. 정사각형 또는 2 차 방정식 (힌트 절 참조)을 완료하여 인수 분해를 사용하여 그래프는 x 축을 교차합니다. 당신은 제로, 하나 또는 두 개의 진짜 뿌리를 얻을 수 있습니다. 그것들을 차트의 포인트로 표시하십시오. 여기서 x 축상의 교차점은 (8/3, 0)과 (-1, 0)입니다.
x 축과 꼭지점을 가로 지르는 'U'모양을 그립니다. 부등식에 등호가 포함되면 실선을 만들고 그렇지 않은 경우 점선을 만듭니다. 원래 방정식이 y>이면 라인 위를 가리 킵니다. 방정식이 y <인 경우 선 아래에 그늘이 있습니다.
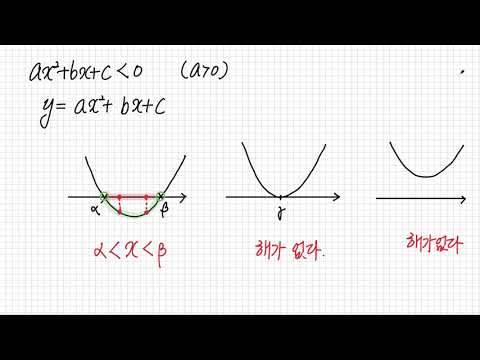
X 축의 크로스 오버와 음영 처리 된 영역을 사용하여 2 차항 불균형에 대한 응답을 결정합니다. 포물선이 내부에 음영 처리되어 있으면 x에 대한 답은 축의 십자가 사이에 있습니다. 예를 들어, y <-3x ^ 2 + 5x + 8 인 경우 그래프의 "U"모양이 위로 향하고 내부가 음영이되어 솔루션이 -1 <x <8/3이됩니다. 음영이 포물선 외부에 있으면 x는 가장 작은 십자가보다 작아야하고 큰 십자가보다 커야합니다. 예는 -3> x> 2입니다.

어떻게

차트에서 점을 계산할 때 x의 값은 수평으로 점의 위치를 나타내고 y의 값은 수직으로 나타냅니다.
x와 0에서 교차점을 풀기 위해 이차 공식을 사용하려면 x = (-b +/- sqrt (b ^ 2 - 4ac)) / 2a) 공식의 계수 a, b 및 c를 대체하십시오. 여기서 'sqrt'는 "제곱근".
음영 위치는 부등식 신호에 따라 달라지며 포물선 오목면이 위 또는 아래를 향하고 있는지 여부가 아닙니다.