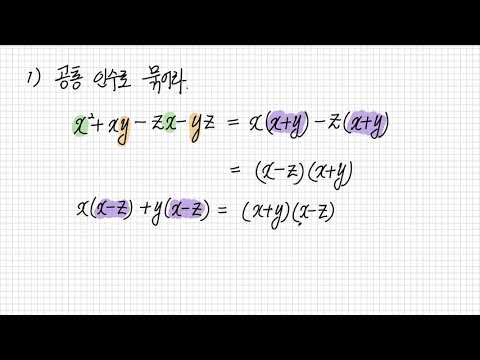
콘텐츠
다항식의 순서는 방정식의 가장 높은 지수 값입니다. 표현식 x ^ 6 + 5x ^ 4 + 1에서 가장 높은 지수는 6이므로 6 차 다항식입니다. 사람들은 4 차 이상의 다항식을 인수 분해하는 것은 쉽지 않지만 하위 순서 표현을 대체하거나 인수 분해하거나 쉽게 분해 가능한 표현식으로 변환하여 인수 분해하는 것은 어려움을 줄이는 데 도움이됩니다.
지침

-
가능한 경우 제기 된 마이너 지수를 높은 전력으로 대체하십시오. 예를 들어 x ^ 6은 (x ^ 2) ^ 3과 같습니다. 따라서 예제는 다음과 같이됩니다. (x ^ 2) ^ 3 + 5 (x ^ 2) ^ 2 + 1. y에 대해 x ^ 2를 대입하면 y ^ 3 + 5y ^ 2 + 1이됩니다. 이제 3 차 다항식을 가지고 있으며이를 해결할 수있는 특정 알고리즘이 있습니다.
-
표현식에서 공통 요소를 가진 용어를 그룹화하고 그 요소를 고려하십시오. 예제에서 x ^ 6 + 2x ^ 5 + 7x + 14의 첫 번째 두 항은 공통 항으로 x ^ 5를 가지며 마지막 두 항은 인자 7을가집니다. x ^ 5 (x + 2) + 7 (x + 2) = (x ^ 5 + 7) (x + 2)이다.
-
2 개의 입방체의 제곱이나 합 또는 차의 차이와 같은 해결 방법을 알고있는 형식으로 다항식을 표현하십시오. 예를 들어, x ^ 6 - x ^ 2 + 6x - 9는 x ^ 6 - (x ^ 2 - 6x + 9)와 같습니다.낮은 차수의 다항식으로 연습 할 때 x ^ 2 - 6x + 9는 (x - 3)의 제곱이라는 것을 알게 될 것입니다. E x ^ 6은 x ^ 3의 제곱입니다. 방정식을 2 개의 제곱의 차이 (x ^ 3) ^ 2 - (x-3) ^ 2로 다시 작성하고 이러한 차이를 인수 분해하기위한 규칙을 사용하십시오.
어떻게
- 학생들은보다 진보 된 연구를하기 전에 연습으로 기본 기술을 습득해야합니다. 고차원 다항식의 인수 분해에 대한 성공은 지식뿐만 아니라 직관과 경험에 기반한 패턴의 인식에 의해서도 달성됩니다.