제곱근 (라디칼)을 단순화하는 방법

작가: Judy Howell
창조 날짜: 2 칠월 2021
업데이트 날짜: 1 12 월 2024
Anonim
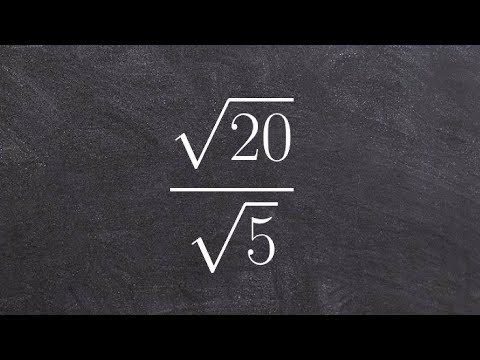
분모를 합리화하여 근본을 단순화하는 방법
동영상: 분모를 합리화하여 근본을 단순화하는 방법

콘텐츠

대수학에서 공통적 인 임무는 라디칼이라고도하는 제곱근을 단순화하는 것입니다. 이 기사에서는 rqd (x)라는 표기법을 사용하여 "x의 제곱근"을 나타냅니다. 때로는 단순화 작업이 매우 간단하지만 다른 경우에는 완벽한 제곱 및 요인에 대한 지식과 함께 특수 수식을 사용해야합니다. 예를 들어, 이것은 rqd (80)와 같은 급진주의 자의 경우입니다. 이것은 급진적 인 것이 단순화되지 않으면 잘못되었다는 것을 의미하며, 시험에서 답을 표시 할 수도 있고 그렇지 않을 수도 있기 때문에 이것은 매우 중요합니다. 이 기사에서는 권한 부여 및 발사의 기본 사항에 익숙하다는 점을 고려합니다.


지침

제곱근의 단순화는 수학에서 중요합니다. (Jupiterimages / Photos.com / 게티 이미지)

  1. rqd (81)처럼 완벽한 사각형 인 급진적 인 표현을 단순화하는 것이 간단합니다. 9²는 81이므로 결과를 얻으려면 계산기를 사용하거나 완벽한 사각형에 대한 지식을 사용할 수 있습니다. 문제의 맥락에서 폐기 될지라도 -9는 문제의 결과이기도합니다. 지오메트리 길이를 포함하거나, 우리가 주 제곱근을 발견하도록 요청 받았다면.

  2. rqd (20)와 같은 불완전한 사각형에서 급진적 인 단순화는 좀 더 많은 작업을 제공합니다. 우리는 계산기를 사용하여 질문의 확장 십진법 근사값을 구할 수 있지만 그것은 급진적 인 것을 단순화하는 것이 아닙니다. 우리가해야 할 일은 요약하면, 급진적 인 것을 분리하는 것입니다. 그래서 우리는 전체의 곱에 첫 번째 숫자의 제곱근을 곱합니다.

  3. 이렇게하기 위해서는 위의 급진파의 특정 특성을 아는 것이 가장 중요합니다. 즉,이 방정식은 제품의 라디칼을 급진파의 산물로 분리 할 수 ​​있음을 나타냅니다. 이 수식을 rqd (20)의 예제에 적용하려면 20을 4와 5로 나눌 필요가 있습니다. 그런 다음 rqd (4x5)를 rqd (4) x rqd (5)로 분리 할 수 ​​있습니다. 우리가 알고있는 rqd (4)는 2이므로 우리의 단순화 된 응답은 2 x rqd (5)입니다. 이것은 시험에서 예상되는 반응입니다. 5가 1과 그 자체로 나눌 수있는 소수이므로 rqd (5)를 어떻게 분해 할 수 없는지 주목하십시오.

  4. 때때로 학생들은 2와 10 같은 다른 요인으로 20을 나눌 수 있는지 물어 봅니다. 답은 우리가 할 수있는 것이지만 rqd (2x10) 일 때 rqd (2) x rqd (10)가됩니다. 어느 쪽도 완벽한 사각형이 아니기 때문에 우리는 우리의 대답에 정수가 없을 것입니다.


  5. 도입부의 rqd (80) 예제로 돌아가 보자. 숫자 80은 2와 40, 4와 20, 8과 10 등과 같이 여러 쌍으로 나눌 수 있습니다. 우리가 찾아야 할 것은 완벽한 80 제곱의 가장 큰 요소이며 그것을 사용하십시오. 숫자 4는 80의 완벽한 제곱 팩터입니다. 그러나 더 큰 숫자가 있습니다. 즉, 우리는 인수 분해에서 16과 5를 사용해야 함을 의미합니다. 우리는 이제 rqd (16 x 5) = rqd (16) x rqd (5) = 4 x rqd (5)를 얻었습니다.

  6. 위의 예제에서 우리의 요소 쌍 중 하나와 함께 40과 20을 사용했다면, rqd (4) x rqd (20)은 2 x rqd (20)와 같을 것이므로 많은 추가 작업이 필요합니다. 그러나 이전에했던 것처럼 rqd (20)를 찾아야합니다. 가장 큰 완벽한 제곱 팩터 인 16을 사용하여 우리는 약간의 반응을 나타 냈습니다.

  7. 다른 예 : rqd (200). 몇 가지 요소가 있으며 그 중 많은 요소가 완벽한 사각형입니다. 우리는 100이라는 가장 큰 완벽한 제곱 팩터를 원합니다. 이는 10 x rqd (2)와 같은 rqd (100) x rqd (2)를 제공합니다.

  8. 프라임 또는 두 소수의 곱인 제곱근을 줄일 수는 없습니다. 예를 들어, 우리는 rqd (13)를 단순화 할 수 없습니다. 완전한 제곱 요소가없는 소수입니다. 우리는 이렇게 답을 남겨야합니다.

    또 다른 예는 rqd (6)입니다. 6 개는 소수가 아닙니다. 우리는 rqd (2) x rqd (3)에서 분리 할 수 ​​있지만, 완벽한 사각형은 없으므로 단순화 할 수 없습니다. 우리는 우리의 답을 rqd (6)로 남겨 둘 것입니다. 완벽한 사각형 요소가 없습니다. 마지막 예는 rqd (77)입니다. 숫자 77은 1 이상의 요소를 가지고 있기 때문에 소수가 아닙니다. 그러나이 다른 요소는 소수입니다. 완벽한 사각형 요소가 없으므로 올바른 대답을 남겨 두어야합니다.